Mates

UNA INMERSIÓN EN EL ALGORITMO ABN
En primer lugar queremos señalar que todo el material aquí insertado está tomado del blog Actiludis. Si pinchas en este ENLACE te llevará a la adecuada introducción y secuenciación del algoritmo ABN.

PARA FAMILIAS Y PROFESADO

 En primer lugar recomendamos ver este pequeño vídeo (FALLO DEL SISTEMA) sobre el fallo del sistema tradicional para comprender mejor el por qué nos introducimos en este nuevo algoritmo.

Sin embargo, para ayudar a nuestro alumnado y a las familias en la tarea de inmersión en el algoritmo ABN
(teniendo en cuenta que no han comenzado el aprendizaje desde Infantil) y que comenzaron el curso pasado en 4º de Primaria iré poniendo las anotaciones o vídeos que, de allí sacados, sean interesantes para su aprendizaje.
PARA EL ALUMNADO


CONTAR
Resultado de imagen de CONTARResultado de imagen de CONTAR


INICIACIÓN EN EL CÁLCULO ESTIMATIVO (blog Actiludis)
Estas series están indicadas para Infantil, Primero de Primaria y para iniciar el cálculo estimativo en cualquier nivel de primaria, al objeto de que vayan creando confianza y familiarizándose con el método.

SERIES DE DIFICULTAD CRECIENTE
Para utilizar en Primaria. También se pueden usar después de las anteriores. Las primeras cuatro series se inician con una más simple que permite que el alumno/a se adapte a la metodología.
SERIES DE 10 A 20 CIFRAS AGRUPADAS
Estas series agrupan las cantidades en dos o tres tipos al objeto de provocar el cálculo mental para alcanzar la solución.


RECTA NUMÉRICA
Resultado de imagen de AMIGOS DEL 10 Y DEL 100 ABNResultado de imagen de TABLA DEL 10 ABN AMIGOS DEL 10

Complementarios o amigos del 10

PINCHA AQUÍ

CASA DEL 100, 1000...
    Resultado de imagen de AMIGOS DEL 100 ABN Resultado de imagen de AMIGOS DEL 100 ABN
TABLA DEL CIEN
CRUCIGRAMA NUMÉRICO PINCHA AQUÍ  

La tabla del 100

Complementarios del 100 y del 1000

Resultado de imagen de AMIGOS DEL 100 ABNPINCHA AQUÍ
Composición y Descomposición de números N
Prezi descomposición
IR AL ENLACE “DESCOMPOSICIÓN Y COMPOSICIÓN NUMÉRICA“

POSIBLE SECUENCIACIÓN EN EDUCACIÓN INFANTIL 3 AÑOS en PDF

GUÍAS RÁPIDAS PARA EL  CÁLCULO EN ABN

 

Guía rápida del cálculo de la suma ABN

 

Guía rápida del cálculo de la resta ABN (detracción)

Guía rápida del cálculo de la resta ABN (Ascendente y descendente)

Guía rápida del cálculo del producto ABN

 

Guía rápida del cálculo de la división ABN

LA SUMA

ABN Cálculo mental: Fases propuestas (Sara Ponce)
> SUMA
Suma Fase 1
Suma Fase 2.1.
Suma Fase 2.2.
Suma Fase 2.4.
Suma Fase 3
Suma Fase 4
Suma Fase 5
Suma Fase 6
Suma Fase 7
Suma Fase 8
Suma Fase 9
Suma Fase 10
Suma Fase 11
Suma Fase 12



 
 ALGORITMO ABN,  SUMA



SOBREPASANDO LA CENTENA
LA RESTA
ABN Cálculo mental: Fases propuestas (Sara Ponce)

RESTA
Resta Fase 2
Resta Fase 3
Resta Fase 4
Resta Fase 5
Resta Fase 6
Resta Fase 7
Resta Fase 8
Resta Fase 9
Resta Fase 10
Resta Fase 11

LA SUMIRRESTA
 

LA DOBLE RESTA
IGUALACIÓN
LA MULTIPLICACIÓN 
El aprendizaje de las tablas es vital para ser ágil en las operaciones. Además practicaremos la tabla extendida.  Entender la estrategia de multiplicar por la unidad seguida de ceros será clave cuando trabaje la estimación, y, sobre todo, la división.

SUBITIZACIÓN

Serie de subitización tabla del 2


TABLAS EXTENDIDAS

MULTIPLICACIÓN FASES RECOMENDADAS PARA EL ESTUDIO DE LAS TABLAS DE MULTIPLICAR
Multiplicación Fase 1
Multiplicación Fase 2
Multiplicación Fase 3
Multiplicación Fase 4
Multiplicación Fase 5
Multiplicación Fase 6
Multiplicación Fase 7

Tabla del 2 extendida
Tabla del 3 extendida
Tabla del 4 extendida
Tabla del 5 extendida
Tabla del 6 extendida
Tabla del 7 extendida
Tabla del 8 extendida
Tabla del 9 extendida
Tabla del 10 extendida
Tabla del 11 extendida
Tabla del 12 extendida

MULTIPLICAR CON DEDOS  
Con las manos tienes las tablas del 6, 7, 8 y 9. Ten en cuenta que el 6 se representa sacando un dedo, el 7 sacando 2, el 8 sacando 3 y el 9 sacando 4. Los que salen se suman, los guardados se multiplican.
Solo hay dos excepciones: el 6x6 y el 6x7.
Si quieres ser ágil en las TABLAS DE MULTIPLICAR aquí te dejamos "EL TANQUE MATEMÁTICO" donde encontrarás un montón de juegos para afianzar tus conocimientos.

Multiplicar por una cifra
Multiplicar por dos cifras
Evolución del caso anterior de multiplicar por dos cifras, en este caso sin descomponer el multiplicador.
El vídeo próximo ilustra la forma de operar cuando hablamos del producto posicional, es decir en función del valor que ocupan los números. Esta forma de operar es la misma que utiliza el ábaco, un recurso milenario.
PARA VER LA MULTIPLICACIÓN POSICIONAL CON DECIMALES IR MÁS ABAJO EN LA SECCIÓN DE NÚMEROS DECIMALES
Para practicar la suma, la resta y la multiplicación con el algoritmo ABN. Pincha eltanquematematico

PROPIEDADES DE LA MULTIPLICACIÓN Y DE LA SUMA
Resultado de imagen de Propiedades de las operacionesPINCHA AQUÍ
LA DIVISIÓN




  Dos cifras en el divisor

Para practicar LA DIVISIÓN con el algoritmo ABN pincha en este enlace. Primero practica escalas y luego divisiones propuestas por el programa o inventadas por ti. Para seguir practicando LA DIVISIÓN con el algoritmo ABN. Pincha en este enlace. 

Multiplica y divide: la unidad seguida de ceros
 
http://www.juntadeandalucia.es/averroes/centros-tic/41009470/helvia/aula/archivos/repositorio/0/193/html/recursos/la/U09/pages/recursos/143304_P121/es_carcasa.html
División por la unidad seguida de ceros 
Unidad ceros
PROPIEDAD FUNDAMENTAL DE LA DIVISIÓN

Eran dos tipos requetefinos
el Dividendo y el divisor
los dos tenían la propiedad
fundamental de la división.
Si al Dividendo y al divisor
multiplicas por un número
mira el cociente que no varía
pero el Resto se multiplicó. 

- Hola Dividendo
- Hola divisor
- Van a multiplicarnos
- Tranquilo, por favor.
- ¿Qué pasa con Cociente?
- Ese no va a cambiar.
- ¿ Y qué le ocurre al Resto?
- Que va a multiplicar.

Eran dos tipos requetefinos
el Dividendo y el divisor
los dos tenían la propiedad
fundamental de la división.

Si al Dividendo y al divisor
les divides por un número
mira el cociente que no varía
pero el Resto se dividió.
- Hola Dividendo
- Hola divisor
- Vienen a dividirnos.
- Tranquilo, por favor.
- ¿Qué pasa con Cociente?
- Ese no va a cambiar.
- ¿ Y qué le ocurre al Resto?
- Dividido quedará.

Representación recta numérica 
Pincha aquí
Comparar decimales
 Aproximar o redondear decimales
Operaciones con decimales

Multiplicación con decimales
Multiplicación con decimales en uno de los factores
 
Multiplicación mental con decimales 
 
Multiplicación con decimales en los dos factores 
 
APRENDER A CAMBIAR DE ORDEN
ARTILUGIO DIDÁCTICO PARA APRENDER A CAMBIAR DE ORDEN






 Sacar números decimales con el algoritmo ABN 
 
División con números decimales en el dividendo
   
 
División de tres cifras con decimales en dividendo
 
División con números decimales en el divisor
 
División con números decimales en el dividendo y en el divisor 



COLOCACIÓN EN EL ALGORITMO TRADICIONAL

Resultado de imagen de suma decimalesResultado de imagen de MULTIPLICACIÓN CON DECIMALES

   Resultado de imagen de DIVISIÓN CON DECIMALES EN DIVISOR

Resultado de imagen de examen
PONTE A PRUEBA
Autoevaluación operaciones con decimales

Autoevaluación:

  1. TEST: LOS NÚMEROS DECIMALES
    ACTIVIDADES DE REPASO I
    1 2 3 4 5 6 7 8 9 10 11 12 13 14
 PORCENTAJES
http://www.eltanquematematico.es/proporcionalidad/proporc_p.html
Aprende sobre porcentajes %
  1. PORCENTAJES I LA CALCULADORA
  2. PORCENTAJES II
  3. PORCENTAJES III
  4. LA CALCULADORA: PORCENTAJES
  5. PORCENTAJE
  6. SD: LA PROPORCIONALIDAD NUMÉRICA: TANTO POR CIENTO
  7. PORCENTAJE II
  8. PROPORCIONALIDAD Y PORCENTAJES
  9. PORCENTAJES IV



MÚLTIPLOS Y DIVISORES

PINCHA AQUÍ


Criterios de divisibilidad

 
PINCHA AQUÍ


PROPIEDADES DE LOS MÚLTIPLOS




PINCHA AQUÍ




CritPINCHA AQUÍ




PINCHA AQUÍ 






DESCOMPOSICIÓN FACTORIAL en factores primos



Actividad 1.

Actividad 2.

Actividad 3.

Actividad 4.

Actividad 5.

Actividad 6.

Actividad 7

LABERINTO DE MÚLTIPLOS Y DIVISORES






NÚMEROS PRIMOS Y COMPUESTOS
Un número PRIMO es aquel que solo tiene como divisores a él mismo y a la unidad (el 1).
Un número COMPUESTO es aquel que tiene otros además de él mismo y la unidad.
Canción de los números primos 
(Música de "La canción de los oficios" de Teresa Rabal)

Me pongo de pie, 
me pongo de pie
me vuelvo a sentar, 
me vuelvo a sentar
porque con los primos 
vamos a jugar. (bis)

Primos son 2 y 3, también el 5 y 7
y con ellos  11, 13, 17 y 19.

Al 23 le sigue un guapo 29
31 y 37 van detrás porque ellos quieren.

 41 está llorando ya de pena 
43 y 47 se lo llevan a la verbena.

Y llega el 53 risueño como ninguno
invita al 59, también al 61.

Viene el 67 con el 71
invitan al 73 a tomar pincho moruno.

79 está con el 83, 
89 y 97 son los primos hasta el 100.

http://www.normaparapensar.com/ldn/sites/default/files/NPM03/captivate2-1.swfPINCHA AQUÍ

Mínimo común múltiplo
PINCHA AQUÍ


ProblemasPINCHA AQUÍ
m.c.mPINCHA AQUÍ

PROBLEMAS 2 

Mínimo Común Múltiplo
PROBLEMAS 3
multiplos odea
POTENCIACIÓN y RADICACIÓN 
Cuadrado de un número
Cuando calculamos el cuadrado de un número cualquiera (n), estamos hallando el área que tendría un cuadrado de lado n:

Diapositiva4
Cuadrados de decenas y semidecenas

Trucos de potenciación para decenas y centenas incompletas
Raíces cuadradas

Algoritmo tradicional Raíces cuadradas 
ECUACIONES DE PRIMER GRADO: Una incógnita


ECUACIONES DE PRIMER GRADO: Dos incógnitas

ORIENTACIÓN ESPACIAL: SIMETRÍA 
Para comprender y practicar qué es la simetría pincha aquí.
TANGRAN EDUCATIVOResultado de imagen de JUEGO CON PALILLOS Juego con palillos.


Medidas de longitud
Longitud.PINCHA AQUÍ




  

MEDIDAS DE SUPERFICIE

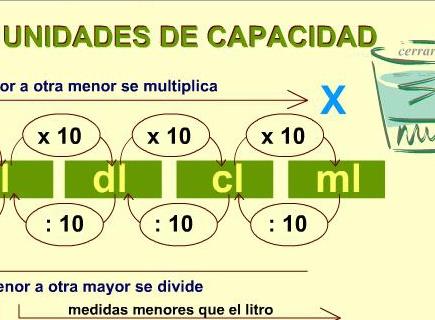
MEDIDAS DE CAPACIDAD












UNIDADES DE VOLUMEN



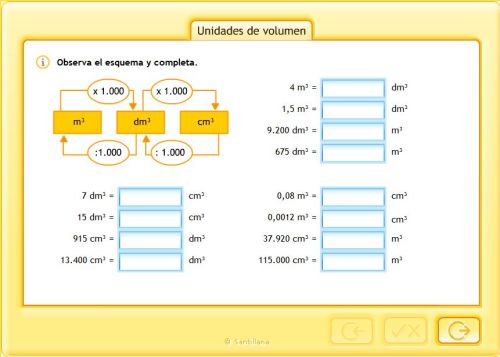PINCHA AQUÍ

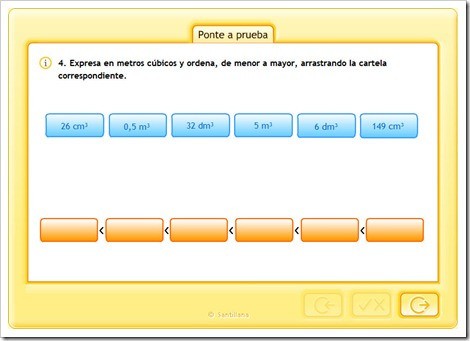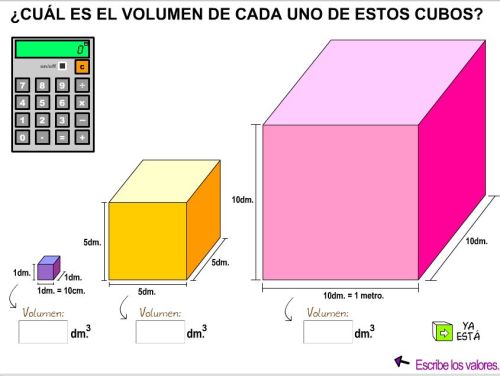PINCHA AQUÍ

 PINCHA AQUÍ

PINCHA AQUÍ

PINCHA AQUÍ

PINCHA AQUÍ

 CÁLCULO MENTAL SERIE PARA 5º Y 6º DE PRIMARIA 
(ALGORITMO TRADICIONAL)

GEOMETRÍA y un poco de historia

EGIPCIOS
El ser humano necesitó contar y por eso creó los números. Quiso hacer cálculos e inventó las operaciones. Hizo relaciones y determinó las propiedades numéricas.
También observó la naturaleza y todo lo que le rodeaba. Por eso ideó líneas, formas, figuras, cuerpos...los que dieron orgien a la geometría.
La palabra geometría viene de geo "tierra" y metría que significa medida, por lo tanto su significado es medir la tierra.
Las primeras ideas para medirla surgieron en Egipto. Allí junto al río Nilo necesitaron remarcar las tierras junto al río que se desbordaban y así controlar las cosechas. Los egipcios aprendieron a medir con cuerdas las áreas de triángulos y rectángulos.
BABILONIOS (las ruinas de Babilonia se encuentran en la actual Irak).
Babilonia era una ciudad de la antigua Mesopotamia. Alcanzó un gran esplendor bajo Hammurabi (s. XVIII a. de C).
Los babilonios también conocían las áreas de los triángulos y los rectángulos sobre todo para resolver problemas de reparto de tierras en las herencias.También conocieron las áreas de los pentágonos, hexágonos y heptágonos. Pero en especial estudiaron mucho el círculo. Eran unos excelentes geometras. Ellos bautizaron las doce constelaciones del zodiaco, dividiendo el círculo zodiacal en 12X30= 360. Junto a la geometría nació, pues, la astronomía. 
 Resultado de imagen de división zodiacal de los babiloniosEste zodiaco les serviría para elaborar calendarios muy útiles para el cultivo de los cereales.
 
De ellos hemos heredado la división de la circunferencia en 360 grados y la de cada grado en 60 minutos y cada minuto en 60 segundos, es decir, el sistema sexagesimal.
 

 GRIEGOS







Quienes dieron carácter científico a la geometría fueron los griegos, ya que incorporaron demostraciones a los razonamientos.
 TALES DE MILETO: se debe a Tales el mérito de haber introducido en Grecia el interés por los estudios geométricos.
   PITÁGORAS:  El símbolo de la escuela de Pitágonas era el pentágono estrellado, que ellos llamaban pentalfa.    
En esta escuela se entraba después de prestar juramento al número 10 y todos los documentos se mantenían de forma oral y nadie podía divulgarlos. Jugaban con piedrecitas y formaban los números cuadrados y los rectangulares. Pitágoras conoció a Tales de Mileto y fueron amigos. Pero Pitágoras fue famoso por su teorema: "Los lados de un triángulo rectángulo forman cuadrados, así dedujo que el cuadrado de la hipotenusa es igual a la suma del cuadrado de los catetos".
 
 

PLATÓNResultado de imagen de euclides matemáticoEUCLIDES
El gran mérito de Euclides fue recopilar los conocimientos matemáticos de la época. Su libro principal se llama "Elementos" y constaba originalmente de trece volúmenes en los que se exponía la geometría clásica. Este libro tiene tanta importancia para las matemáticas como el "Principia" de Newton para la física o "La evolución de las especies" de Darwin para la biología.
Para sentar las bases de la geometría formuló cinco postulados a través de los cuales se dedujo toda la geometría de la época.
Los cinco postulados eran:
1) Si tenemos dos puntos, podemos dibujar una recta que los una.
2) Cualquier recta se hacer todo lo larga que se quiera.
3) Se puede trazar una circunferencia de cualquier tamaño alrededor de cualquier punto.
4)Todos los ángulos rectos son iguales.
5) Si tenemos una recta y un punto externo a ella, podremos dibujar todas las rectas que queramos que pasen por ese punto, pero solo una de ellas será paralela a la que ya teníamos.

 (Información sacada del blog
http://poligonos1.blogspot.com.es/)

Después de Euclides tuvieron que pasar muchos años para que surgieran matemáticos que discreparan de sus postulados (del quinto concretamente) y así surgieron otras geometrías, ya que en una esfera al geometría no es igual que en un plano.
INTRODUCCIÓN A LA GEOMETRÍA

 

                                              





No hay comentarios:

Publicar un comentario

Suscribirse a: Entradas (Atom)